运输问题

运输问题的数学模型

运输问题的一般提法：

研究单一品种物资的运输调度问题，其典型情况是：设某种物品有m个产地$(A_1,A_2,\cdots,A_m)$,各产地的产量分别是$(a_1,a_2,\cdots,a_m)$；有n个销地$(B_1,B_2\cdots,B_n)$，各销地的销量分别为$(b_1,b_2,\cdots,b_n)$。假定从产地$A_i(i=1,2,\cdots,m)$向销地$B_j(j=1,2,\cdots,n)$运输单位物品的运价是$c_{ij}$。根据产销关系可以将运输问题分为以下三种类型：

$$\displaystyle \sum_{i=1}^m a_i = \sum_{j=1}^n b_j\quad \text{产销平衡问题} \\ \displaystyle \sum_{i=1}^m a_i > \sum_{j=1}^n b_j\quad \text{供过于求问题} \\ \displaystyle \sum_{i=1}^m a_i < \sum_{j=1}^n b_j\quad \text{供不应求问题} \\$$

重点考察产销平衡问题，用$x_{ij}$表示从$A_i$到$B_j$的运量，那么在产销平衡的条件下，以运费最小为目标的运输问题模型可以表示为：

$$\min_{}\ z\ =\ \displaystyle \sum_{i=1}^m\sum_{j=1}^n c_{ij}x_{ij} \\ s.t. \begin{cases} \displaystyle \sum_{j=1}^n x_{ij}=a_i\ ,\ (i=1,2,\cdots,m) \\ \displaystyle \sum_{i=1}^m x_{ij}=b_j\ ,\ (j=1,2,\cdots,n) \\ x_{ij} \ge 0\ ,\ (i=1,2,\cdots,m\ ;\ j=1,2,\cdots,n) \end{cases}$$

运输问题模型特点：

• 运输问题有有限最优解
• 运输问题约束条件的系数矩阵
  • 约束条件系数矩阵的元素等于1或0
  • 约束条件系数矩阵的每一列有两个非零元素，这对应了每一个变量在前m个约束方程中出现一次，在后n个约束方程中出现一次
  • 对于产销平衡运输问题，还有以下特点：
    • 所有约束条件结构都是等式约束
    • 各产地产量之和等于各销地销量之和
• 运输问题模型中包含$m\times n$个变量，$(m+n)$个约束条件，但因为有$\displaystyle \sum_{i=1}^m a_i = \sum_{j=1}^n b_j$，所以系数矩阵中 线性独立的列向量的最大个数为$(m+n-1)$个，即运输问题的解中的 基变量数不多于$(m+n-1)$个。

---

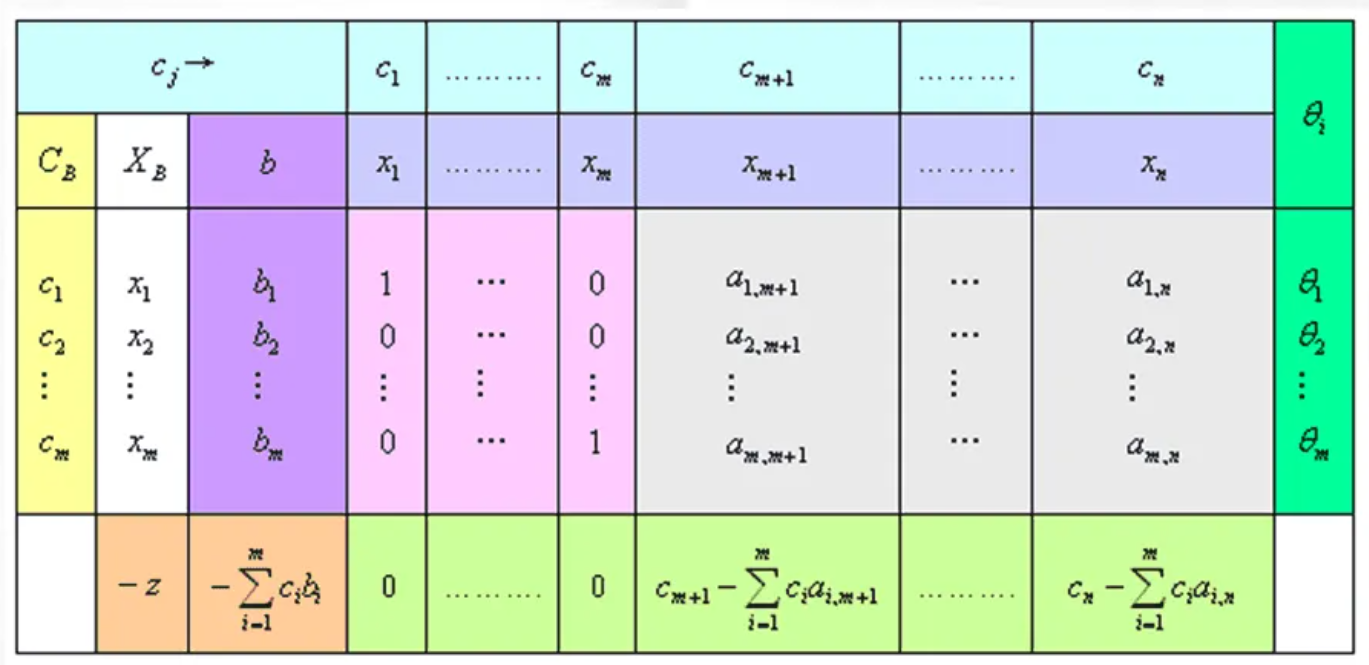
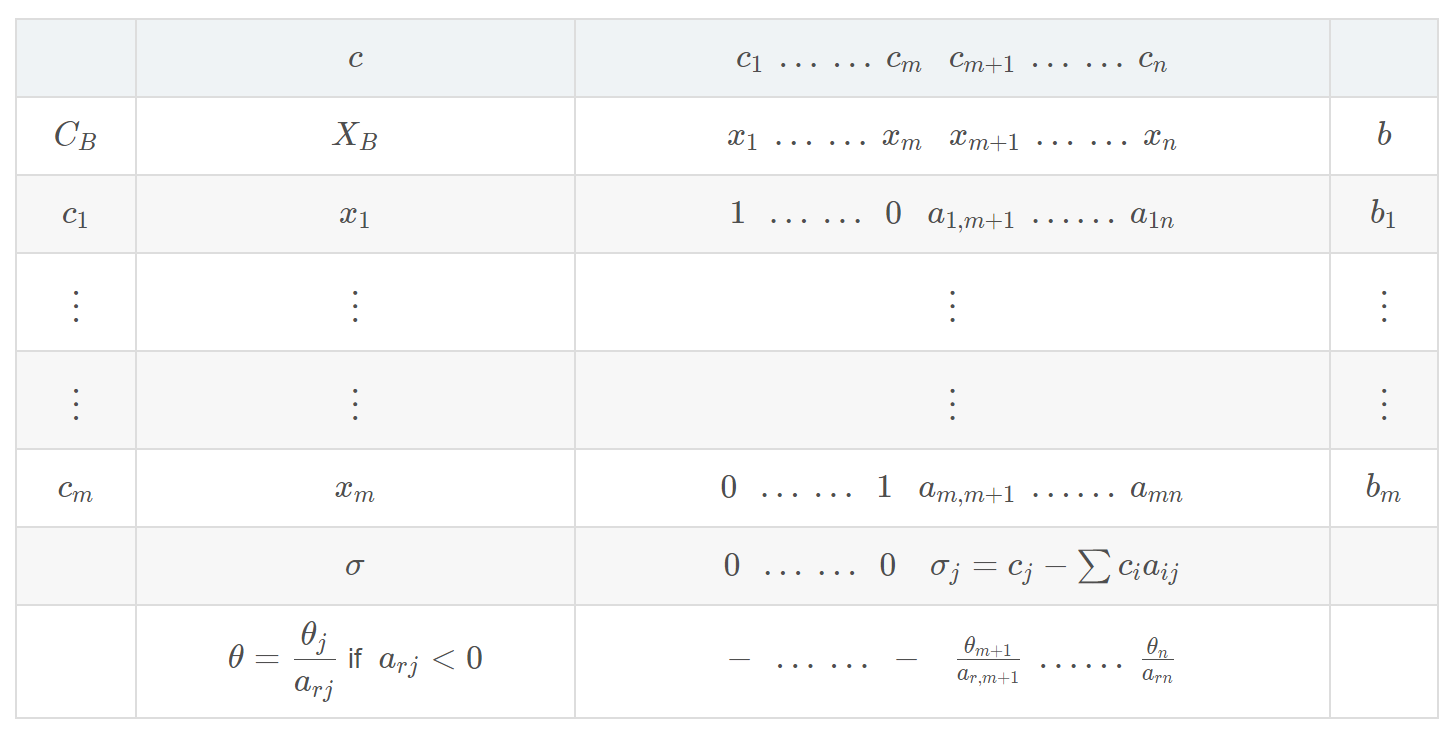
表上作业法

求解步骤：

1. 初始方案的给定（确定初始基可行解）

   1. 最小元素法
      • 基本思路：运价最低者为优先原则，安排初始的调运方案
      • 规则：从运价最小的开始，在该格标上允许取得的最大数量。然后继续按照运价从小到大顺序填数，若某行（列）的产量（销量）以满足需求，则把该行（列）的产量（销量）的其它格去掉。重复上述方法进行下去，直到得到一个基本可行解。
      • 缺点：最小元素法只从局部观点考虑就近供应，可能造成总体的不合理
   2. Vogel 法
      • 从运价表上分别找出每行与每列的最小的两个元素之差
      • 再从差值最大的行或列中找出最小运价确定供需关系和供应数量。当产地或销地中有一方数量上供应完毕或得到满足时，划去运价表中对应的行和列
      • 重复上述步骤，直到产地的产量分配完、销地的销量得到满足时为止。
      • 一般情况下当 产销地的数量不多时，Vogel法给出的初始方案可能就是最优方案，所以 Vogel 法有时就用作求运输问题最有方案的近似解。

2. 最优性检验
   由于运输问题目标函数求的是极小值，因此当所有非基变量的检验数均大于等于零时，则基本可行解为最优解，否则需要进一步调整。

   1. 闭回路法

   运输问题的闭回路是指 调运方案中由一个空格和若干个有效数字格的水平和垂直连线包围成的封闭回路
   构建闭回路的目的时要计算解中各非基变量（对应空格）的检验数。方法是令某非基变量的取值为1，通过变化原基变量的值找出一个新的可行解，将其同原来的基可行解目标函数值作比较。

   通过构建的闭回路计算空格对应的非基变量的检验数
   $\sigma_{ij}=$ 闭回路上第奇数个顶点单位运费之和 - 闭回路上第偶数个顶点单位运费之和。（其中非基变量为第一个顶点）
   一定要是闭回路的顶点才可以参与计算，边途径的点不算

   缺点：当一个运输问题的产地和销地数量很多事，构建闭回路的工作繁重。

   2. 位势法
      • 作表将有效数字换成运价表上对应格的运价
      • 分别在表的下侧添加$v_j(j=1,2,\cdots,n)$，右侧添加$u_i(i=1,2,\cdots,m)$使得表中的有效数字都刚好等于它所在行和列的这些新填数字之和。（这些新添加的数字可以自己赋值）
      • 利用闭回路法可以得任意空格（非基变量）得检验数字为 $\sigma_{ij}=c_{ij}-(u_i+v_j)$，其中$c_{ij}$是该格对应得单位运价表的运价。

3. 方案调整改进

   • 从检验数为负值得格出发（当有两个以上负检验数时，从 绝对值 最大的负检验数格出发），做一条除了该空格以外其余顶点均为有效数字组成的闭回路。在这条闭回路上，对 运量 作最大可能的调整。
   • 在该闭回路上，偶数顶点调运量的最小值为调整量 θ，其对应的基变量就是出基变量
   • 调整：在该闭回路上，奇数顶点运输量的数值均加上调整量 θ，偶数顶点均减去调整量 θ。则出基变量经过调整后必定为0，该变量由基变量变为非基变量。除此之外，其他顶点运输量保持不变。

---

产销不平衡的运输问题

实际问题中产销往往是不平衡的，讨论供过于求问题。
当$\displaystyle \sum_{i=1}^m a_i > \sum_{j=1}^n b_j$（产大于销）时，运输问题数学模型如下所示

$$\min_{}\ z =\ \displaystyle \sum_{i=1}^m \sum_{j=1}^n c_{ij}x_{ij} \\ s.t. \begin{cases} \displaystyle \sum_{j=1}^n x_{ij} \le a_i \quad (i=1,2,\cdots,m)\\ \displaystyle \sum_{i=1}^m x_{ij} = b_j \quad (j=1,2,\cdots,n)\\ x_{ij} \ge 0 \end{cases}$$

由于总的产量大于销量，需要考虑多余的物资在哪一个产地就地库存的问题。
设 $x_{i,n+1}$ 是产地 $A_i$ 的库存量，于是有

$$\sum_{j=1}^n x_{ij} + x_{i,n+1} = \sum _{j=1}^{n+1}x_{ij} = a_i \quad (i=1,2,\cdots,m) \\ \sum_{i=1}^m x_{ij} = b_j \quad (j=1,2,\cdots,n)\\ \sum_{i=1}^m x_{i,n+1}=\sum_{i=1}^m a_i - \sum_{j=1}^n b_j = b_{n+1}$$

令

$$c^{'}_{ij} = c_{ij} \quad (i=1,\cdots,m;j=1,\cdots,n)\\ c^{'}_{ij} = 0 \quad (i=1,\cdots,m;j=1,\cdots,n+1)$$

将上述式子代入运输问题数学模型中得到新模型

$$\min_{}\ z^{'}\ =\ \sum_{i=1}^m\sum_{j=1}^{n+1} c^{'}_{ij}x_{ij}=\sum_{j=1}^n c^{'}_{ij}x_{ij} + \sum_{i=1}^{m}c^{'}_{i.n+1}s_{ij}=\sum_{j=1}^n c_{ij}x_{ij}\\ s.t. \begin{cases} \displaystyle \sum_{j=1}^{n+1} x_{ij}=a_i\ ,\ (i=1,2,\cdots,m) \\ \displaystyle \sum_{i=1}^m x_{ij}=b_j\ ,\ (j=1,2,\cdots,n) \\ x_{ij} \ge 0\ ,\ (i=1,2,\cdots,m\ ;\ j=1,2,\cdots,n) \end{cases}$$

可以很明显地看出得到的新模型是一个产销平衡地运输问题模型

当供过于求时，只要增加一个假想地销地$j = n+1$（实际上是库存），该销地的总需量为$\displaystyle \sum_{i=1}^m a_i - \sum_{j=1}^n b_j$，而在单位运价表中从个产地到假想销地的单位运价为$c^{'}_{i,n+1} = 0$，于是元运输问题就转换成一个产销平衡的运输问题。
类似的，当供不应求时，可以在增加一个假想的产地$i=m+1$，该产地产量为$\displaystyle \sum_{j=1}^n b_j - \sum_{i=1}^m a_i$，在单位运价表上令从该假想产地到各销地的运价为$c^{'}_{m+1,j} = 0$,同样也可以转换成一个产销平衡问题