线性回归--LDA

线性判别分析-LDA

重点考概念、是什么，以及重要结论推导。

$LDA$ 是一种 数据降维 的方法，与 $PCA$ 不同的是，$LDA$ 属于 监督学习，也就是说它的数据集是带标签的

有关 $LDA$ 的分布基本知识以及在 $NLP$ 上的应用 一文详解LDA主题模型

基本思想

$LDA$ 的基本思想：给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近、异类样例的投影点中心尽可能远离。

更简单的概括为一句话，就是 “投影后类内方差最小，类间方差最大”。

可能还是有点抽象，这里以最简单的二分类为例子，欲将二维数据降成一维数据：

举个栗子

$e.g.$

假设我们有两类数据分为 $+$ 和 $-$，如下图所示，这些数据特征是二维的，我们希望将这些数据投影到一维的一条直线，让每一种类别数据的投影点尽可能的接近，而 $+$ 和 $-$ 数据中心之间的距离尽可能的大。（图源：《机器学习》–周志华

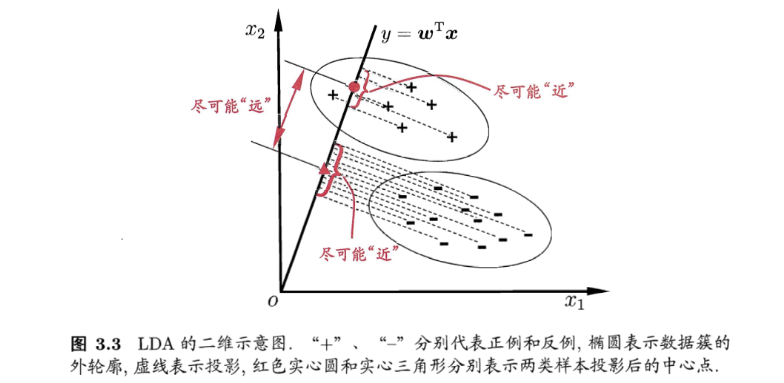
我们将这个最佳的向量称为 $w$ ，那么样例 $x$ 到方向向量 $w$ 上的投影可以用下式来计算

$$y = w^T x$$

当 $x$ 是二维的时候，我们就是要找一条直线（方向为 $w$ ）来做投影，然后寻找最能使样本点分离的直线。

（这部分得硬着头皮啃下来

目标函数的构建（99%

接下来我们从定量的角度来找到这个最佳的 $w$。

给定数据集 $D=\left\{\left(x_{i}, y_{i}\right)\right\}_{i=1}^{m}, y_{i} \in\{0,1\}$ , 令 $N_{i} 、 X_{i} 、 \mu_{i} 、 \Sigma_{i}$ 分别表示第 $i \in\{0,1\}$ 类示例的样本个数、样本集合、均值向量、协方差矩阵。

其中：

$$\mu_{i}=\frac{1}{N_{i}} \sum_{x \in X_{i}} x(i=0,1) \\ \Sigma_{i}=\sum_{x \in X_{i}}\left(x-\mu_{i}\right)\left(x-\mu_{i}\right)^{\top}(i=0,1)$$

类间样本中心点距离尽量远

由于是两类数据, 因此我们只需要将数据投影到一条直线上即可。

假设我们的投影直线是向量 $w$ , 则对任意一个样本 $x_{i}$ , 它在直线 $w$ 的投影为 $w^{\top} x_{i}$ , 对于我们的两个类别的中心点 $u_{0}$, $u_{1}$ , 在 直线 $w$ 的投影为 $w^{\top} \mu_{0}$ 和 $w^{\top} \mu_{1}$ , 分别用 $\tilde{\mu_{0}}$ 和 $\tilde{\mu_{1}}$ 来表示。

那么什么是最佳的 $w$ 呢?

首先发现, 能够使投影后的 两类样本中心点尽量分离 的直线是好的直 线, 定量表示就是:

$$\arg _{\max _{w}} J(w)=\left\|\boldsymbol{w}^{\top} \mu_{0}-w^{\top} \mu_{1}\right\|_{2}^{2}=\left\|\tilde{\mu_{0}}-\tilde{\mu_{1}}\right\|_{2}^{2}$$

类内样本点方差尽量小

不能仅仅考虑样本中心的距离：

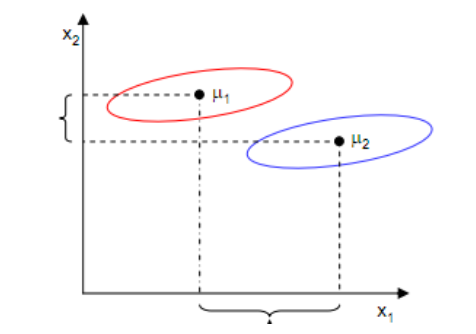
如上图，样本点均匀分布在椭圆里，投影到横轴 $x_1$ 上时能够获得更大的中心点间距 $J(w)$ ，但是由于投影后两类样本有重叠， $x_1$ 不能分离样本点。投影到纵轴 $x_2$ 上，虽然 $J(w)$ 较小，但是能够分离样本点。

因此我们还需要考虑同类样本点之间的方差，同类样本点之间方差越小， 就越难以分离。

这里引入另外一个度量值, 称作散列值 $( scatter)$, 对投影后的类求散列值, 如下:

$$\tilde{S}^{2}=\sum_{x \in X_{i}}\left(w^{\top} x-\tilde{\mu_{i}}\right)^{2}$$

从公式中可以看出, 只是少除以样本数量的方差值, 散列值的几何意义是样本点的密集程度, 值越大，越分散，反之越集中。
而我们想要的投影后的样本点的样子是: 不同类别的样本点越分开越好, 同类的越聚集越好, 也就是 均值差越大越好, 散列值越小越好。

正好, 我们同时考虑使用 $J(w)$ 和 $S$ 来度量, 则可得到欲最大化的目标：（关于目标函数为什么是比值形式而不是差值形式，文末总结处会给出我自己的观点。）

$$J(w)=\frac{\left\|w^{\top} \mu_{0}-w^{\top} \mu_{1}\right\|_{2}^{2}}{\tilde{S}_{0}{ }^{2}+\tilde{S}_{1}{ }^{2}}$$

目标函数分子（样本点中心距离）越大，分母（类间样本点方差）越小。

求解最优目标函数（99%

确定目标函数后，接下来的事就比较明显了，我们只需寻找使 $J(w)$ 最大的 $w$ 即可。

首先对目标函数进行改写。（wsp口中的美妙的式子

改写目标函数

（复习的时候看懂后确实感觉挺妙的，美就算了

（还有啊，ppt上面那堆是个什么鬼啊，一大坨一大坨的，生怕我们看懂是吧。

ba说了，开始。

先把散列值公式展开：

$$\tilde{S}^{2}=\sum_{x \in X_{i}}\left(w^{\top} x-\tilde{u_{i}}\right)^{2}=\sum_{x \in X_{i}} w^{\top}\left(x-\mu_{i}\right)\left(x-\mu_{i}\right)^{\top} w$$

我们定义上式展开中的中间那部分如下：

$$\Sigma_{i}=\sum_{x \in X_{i}}\left(x-\mu_{i}\right)\left(x-\mu_{i}\right)^{\top}$$

这个公式的样子不就是少除以样例数的协方差矩阵么，称为 散列矩阵（$scatter\ matrices$）。

继续定义“类内散度矩阵”（$within-class\ scatter\ matrix$）$S_w$：

$$S_{w}=\Sigma_{0}+\Sigma_{1}$$

以及 “类间散度矩阵” ($between-class\ scatter\ matrix$) $S_{b}$ ：

$$\begin{array}{l} \left\|w^{\top} \mu_{0}-w^{\top} \mu_{1}\right\|_{2}^{2}=w^{\top}\left(\mu_{0}-\mu_{1}\right)\left(\mu_{0}-\mu_{1}\right)^{\top} w \\ S_{b}=\left(\mu_{0}-\mu_{1}\right)\left(\mu_{0}-\mu_{1}\right)^{\top} \end{array}$$

因此，则 $J(w)$ 可以重写为：

$$J(w)=\frac{w^{\top} S_{b} w}{w^{\top} S_{w} w}$$

（美不美，美不美，美不美，nnd美的毛

这就是 $LDA$ 欲最大化的目标。即 $S_{b}$ 与 $S_{w}$ 的 “广义瑞利商” ($generalized\ Rayleigh\ quotient$)。

如何确定 w 呢？

当然是抓阄确定啊！

开玩笑开玩笑，这玩意人工智能里面也考过了。这里ppt倒是讲的很清楚，我就直接搬过来了。

观察发现：上式问题的 $w$ 并不是唯一的，倘若 $w$ 对应 $J(w)$ 的极大值点，则 $a*w$ 仍然可以达到 $J(w)$ 的极大值点

因此问题转化为：

$$\arg \max _{w} J_{b}(w)=w^{T} S_{b} w \text {, 使得 } w^{T} S_{w} w=1 \text {. }$$

构造拉格朗日函数：

$$\mathcal{L}(w, \lambda)=w^{T} S_{b} w-\lambda\left(w^{T} S_{w} w-1\right)$$

对拉格朗日函数求偏导并设其偏导数为零, 得：

$$\frac{\partial \mathcal{L}}{\partial w}=2 S_{b} w-2 \lambda S_{w} w=0$$

如果 $S_w$ 可逆, 那么：

$$S_{w}^{-1} S_{b} w=\lambda w .$$

结论：

最优 $w$ 就是 $S_{w}^{-1} S_{b}$ 的 特征向量, 而这个公式也 称为 $Fisher$ 线性判别。

python实现（虚晃一枪

实现就麦油啦，我也没手写过，直接掉库的，关键他也不考嘿嘿。

总结

LDA 和 PCA

$PCA$（主成分分析）和 $LDA$（线性判别分析）有很多的相似点，其本质是要将初始样本映射到维度更低的样本空间中，但是 $PCA$ 和 $LDA$ 的 映射目标 不一样：

• $PCA$ 是为了让映射后的样本具有最大的 发散性；
• 而 $LDA$ 是为了让映射后的样本有最好的 分类性能。

所以说 $PCA$ 是一种无监督的降维方法，而 $LDA$ 是一种有监督的降维方法。

优缺点

优点：

• 在降维过程中可以使用类别的先验知识经验，而像 $PCA$ 这样的无监督学习则无法使用类别先验知识。
• $LDA$ 在样本分类信息 依赖均值而不是方差的时候，比 $PCA$ 之类的算法较优。

缺点：

• $LDA$ 不适合对 非高斯分布 样本进行降维，$PCA$ 也不适用
• $LDA$ 降维最多降到类别数 $k-1$ 的维数，如果我们降维的维度大于 $k-1$，则不能使用 $LDA$ （后面会解答
• 样本分类信息 依赖方差而不是均值时，$LDA$ 降维效果欠佳
• $LDA$ 可能过度拟合数据

几个问题

1、可不可以用均值之差而不是类间散布。

可以，这样做更符合直觉，并且更容易求解。

但是采用 类间散布 的话可以把 $LDA$ 的目标函数表达成 广义瑞利商（就是那个美妙的式子，记得吗），并且上下齐次更加合理。可能是因为这些原因，经典 $LDA$ 最终选择了类间散布。

2、可不可以把 $K$ 类 $LDA$ 投影到大于 $K-1$ 维的子空间中。

不可以，因为 类间散布矩阵的秩不足。

$K$ 类 $LDA$ 只能找到 $K-1$ 个使目标函数增大的 特征值对应的特征向量，即使选择了其他特征向量，我们也无法因此受益。

3、可不可以用类间散布与类内散布的差值，而不是比值。

这里给出两个解释：

• wsp上课是说，目标函数上下界的问题，因此不采用差值而是比值
• 我的理解是可以的：在新准则下可以得到新的最优解，但是我们无法因此受益，$K$ 类 $LDA$ 还是只能投影到 $K-1$ 维空间中。差值版 $LDA$ 与比值版 $LDA$ 相比还缺少了一个 直觉解释，可能是因为这些原因，经典 $LDA$ 最终选择了比值。

简单来说，我觉得都是大佬的直觉哈哈哈