朴素贝叶斯–Navie Bayes
考察计算、徒手构建,不考察证明(芜湖
说实话这部分他会考啥我真没想法
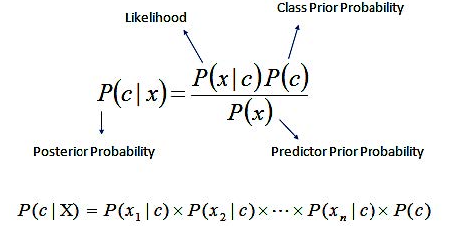
朴素贝叶斯 (N a v i e B a y e s Navie\ Bayes N a v i e B a yes 有监督 的学习算法,解决的是 分类问题
贝叶斯理论基本思想
基于先验知识,根据一些随机出现或观察到的现象来判断事物真相,原因或未知,就有一定的不确定性。
任何未知的判断或推测都是是不确定的,如何用一个概率分布去描述,也即未知的不确定性程度由先验概率分布和现象出现的概率分布。
需要做多次检测和由具有不同个人主观经验的人来判断,然后按照极大似然原则选择结果。
先验信息可以通过收集、挖掘和加工而量化,形成先验分布
概率分布基础(99%
条件概率
B B B A A A
P ( A ∣ B ) = P ( A ∩ B ) P ( B ) P ( A ∩ B ) = P ( A ∣ B ) P ( B ) P(A \mid B)=\frac{P(A \cap B)}{P(B)} \\
P(A \cap B)=P(A \mid B) P(B)
P ( A ∣ B ) = P ( B ) P ( A ∩ B ) P ( A ∩ B ) = P ( A ∣ B ) P ( B )
同理:
P ( A ∩ B ) = P ( B ∣ A ) P ( A ) P(A \cap B)=P(B \mid A) P(A)
P ( A ∩ B ) = P ( B ∣ A ) P ( A )
整理可得条件概率转换计算公式:
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A \mid B)=\frac{P(B \mid A) P(A)}{P(B)}
P ( A ∣ B ) = P ( B ) P ( B ∣ A ) P ( A )
全概率公式
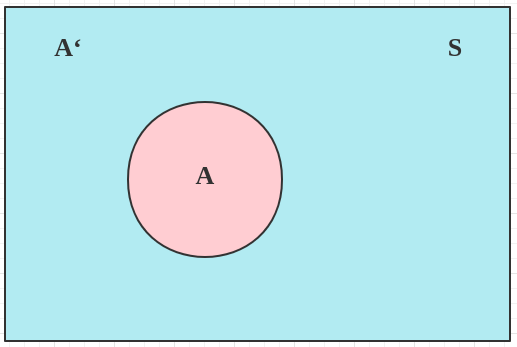
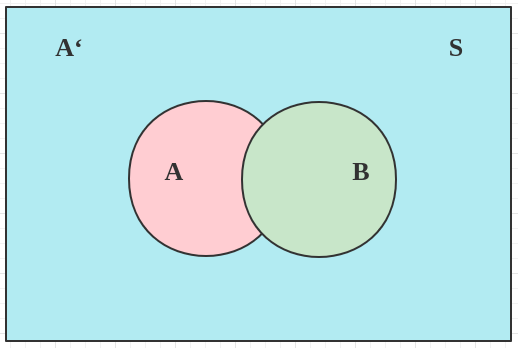
假定样本空间 S S S A , A ′ A, A' A , A ′
在这种情况下,引入事件 B B B B B B
P ( B ) = P ( B ∩ A ) + P ( B ∩ A ′ ) P(B)=P(B \cap A)+P\left(B \cap A^{\prime}\right)
P ( B ) = P ( B ∩ A ) + P ( B ∩ A ′ )
由条件概率公式可知:
P ( B ∩ A ) = P ( B ∣ A ) P ( A ) P(B \cap A)=P(B \mid A) P(A)
P ( B ∩ A ) = P ( B ∣ A ) P ( A )
所以 P ( B ) P(B) P ( B )
P ( B ) = P ( B ∣ A ) P ( A ) + P ( B ∣ A ′ ) P ( A ′ ) P(B)=P(B \mid A) P(A)+P\left(B \mid A^{\prime}\right) P\left(A^{\prime}\right)
P ( B ) = P ( B ∣ A ) P ( A ) + P ( B ∣ A ′ ) P ( A ′ )
这就是全概率公式。它的含义是,如果 A A A A ′ A' A ′ B B B A A A A ′ A' A ′ B B B
结合条件概率公式,可以得到概率公式的另一种表示方法:
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ∣ A ) P ( A ) + P ( B ∣ A ′ ) P ( A ′ ) P(A \mid B)=\frac{P(B \mid A) P(A)}{P(B \mid A) P(A)+P\left(B \mid A^{\prime}\right) P\left(A^{\prime}\right)}
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) + P ( B ∣ A ′ ) P ( A ′ ) P ( B ∣ A ) P ( A )
朴素贝叶斯理论
朴素贝叶斯是贝叶斯决策理论的一部分
贝叶斯决策理论
假设现在有一个数据集 D = ( X , Y ) D=(X,Y) D = ( X , Y )
用 P i ( x , y ) , ( i = 1 , 2 ) P_i(x,y), (i = 1,2) P i ( x , y ) , ( i = 1 , 2 ) ( x , y ) (x,y) ( x , y )
当 P 1 ( x , y ) > P 2 ( x , y ) P_1(x,y) > P_2(x,y) P 1 ( x , y ) > P 2 ( x , y )
当 P 1 ( x , y ) < P 2 ( x , y ) P_1(x,y) < P_2(x,y) P 1 ( x , y ) < P 2 ( x , y )
也就是说,我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想,即选择具有最高概率的决策。
(挺那啥的哈哈哈
贝叶斯推断(99%
整理后的条件概率转换公式如下:
P ( A ∣ B ) = P ( A ) P ( B ∣ A ) P ( B ) P(A \mid B)=P(A) \frac{P(B \mid A)}{P(B)}
P ( A ∣ B ) = P ( A ) P ( B ) P ( B ∣ A )
下面给出几个概念:
P ( A ) P(A) P ( A ) “先验概率”(P r i o r p r o b a b i l i t y Prior\ probability P r i or p ro babi l i t y ,即在 B B B A A A P ( A ∣ B ) P(A|B) P ( A ∣ B ) “后验概率”(P o s t e r i o r p r o b a b i l i t y Posterior\ probability P os t er i or p ro babi l i t y ,即在 B B B A A A P ( B ∣ A ) / P ( B ) P(B|A)/P(B) P ( B ∣ A ) / P ( B ) “可能性函数”(L i k e l y h o o d Likelyhood L ik e l y h oo d ,这是一个调整因子,使得预估概率更接近真实概率。
因此条件概率可以理解成一下公式:
这就是贝叶斯推断的含义。我们先预估一个"先验概率",然后加入实验结果,看这个实验到底是增强还是削弱了"先验概率",由此得到更接近事实的"后验概率"。
如果"可能性函数" P ( B ∣ A ) / P ( B ) > 1 P(B|A)/P(B)>1 P ( B ∣ A ) / P ( B ) > 1 A A A
如果"可能性函数" = 1 =1 = 1 B B B A A A
如果"可能性函数" < 1 <1 < 1 A A A
朴素贝叶斯推断(99%
贝叶斯和朴素贝叶斯的概念是不同的,区别就在于“朴素”二字。
朴素贝叶斯 对条件个概率分布做了条件独立性的假设 。什么意思捏
假设事件 X X X n n n
P ( a ∣ X ) = p ( X ∣ a ) p ( a ) = p ( x 1 , x 2 , x 3 , … x n ∣ a ) p ( a ) \mathrm{P}(\mathrm{a} \mid \mathrm{X})=\mathrm{p}(\mathrm{X} \mid \mathrm{a}) \mathrm{p}(\mathrm{a})=\mathrm{p}\left(x_{1}, x_{2}, x_{3}, \ldots x_{n} \mid \mathrm{a}\right) \mathrm{p}(\mathrm{a})
P ( a ∣ X ) = p ( X ∣ a ) p ( a ) = p ( x 1 , x 2 , x 3 , … x n ∣ a ) p ( a )
由于每个特征都是独立的,我们可以进一步拆分公式 :
p ( a ∣ X ) = p ( X ∣ a ) p ( a ) = { p ( x 1 ∣ a ) ∗ p ( x 2 ∣ a ) ∗ p ( x 3 ∣ a ) ∗ … ∗ p ( x n ∣ a ) } p ( a ) \begin{aligned}
\mathrm{p}(\mathrm{a} \mid \mathrm{X})&= \mathrm{p}(\mathrm{X} \mid \mathrm{a}) \mathrm{p}(\mathrm{a}) \\
& =\left\{\mathrm{p}\left(\mathrm{x}_{1} \mid a\right) * \mathrm{p}\left(\mathrm{x}_{2} \mid a\right) * \mathrm{p}\left(\mathrm{x}_{3} \mid a\right) * \ldots * \mathrm{p}\left(\mathrm{x}_{n} \mid \mathrm{a}\right)\right\} \mathrm{p}(\mathrm{a})
\end{aligned}
p ( a ∣ X ) = p ( X ∣ a ) p ( a ) = { p ( x 1 ∣ a ) ∗ p ( x 2 ∣ a ) ∗ p ( x 3 ∣ a ) ∗ … ∗ p ( x n ∣ a ) } p ( a )
简单来说就是可以 连乘 啦
简单而言,对于给定的训练数据,朴素贝叶斯先基于特征条件独立假设学习输入和输出的联合概率分布,然后基于此分布对于新的实例,利用贝叶斯定理计算出最大的后验概率。朴素贝叶斯不会直接学习输入输出的联合概率分布,而是通过学习类的先验概率 和类条件概率 来完成。
所谓朴素贝叶斯中朴素的含义,即特征条件独立假设,条件独立假设就是说用于分类的特征在类确定的条件下都是条件独立的。这一假设使得朴素贝叶斯的学习成为可能。
朴素贝叶斯算法步骤(50%
为什么是 50 % 50\% 50%
1、计算类先验概率
类先验概率可直接用极大似然估计进行计算。
p ( y = c k ) = 1 N ∑ i = 1 N I ( y ~ i = c k ) , k = 1 , 2 , ⋯ , K p\left(y=c_{k}\right)=\frac{1}{N} \sum_{i=1}^{N} I\left(\tilde{y}_{i}=c_{k}\right), k=1,2, \cdots, K
p ( y = c k ) = N 1 i = 1 ∑ N I ( y ~ i = c k ) , k = 1 , 2 , ⋯ , K
2、计算类条件概率:
p ( x j = a j , l ∣ y = c k ) = ∑ i = 1 N I ( x i , j = a j , l , y ~ i = c k ) ∑ i = 1 N I ( y ~ i = c k ) j = 1 , 2 , ⋯ , n ; l = 1 , 2 , ⋯ , s j ; k = 1 , 2 , ⋯ , K \begin{array}{c}
p\left(x_{j}=a_{j, l} \mid y=c_{k}\right)=\frac{\sum_{i=1}^{N} I\left(x_{i, j}=a_{j, l}, \tilde{y}_{i}=c_{k}\right)}{\sum_{i=1}^{N} I\left(\tilde{y}_{i}=c_{k}\right)} \\
j=1,2, \cdots, n ; l=1,2, \cdots, s_{j} ; k=1,2, \cdots, K
\end{array}
p ( x j = a j , l ∣ y = c k ) = ∑ i = 1 N I ( y ~ i = c k ) ∑ i = 1 N I ( x i , j = a j , l , y ~ i = c k ) j = 1 , 2 , ⋯ , n ; l = 1 , 2 , ⋯ , s j ; k = 1 , 2 , ⋯ , K
3、给定新的实例,计算其对应的最大后验概率,然后判断其所属的类别:
y ^ = arg max c k p ( y = c k ) ∏ j = 1 n p ( x j ∣ y = c k ) \hat{y}=\arg \max _{c_{k}} p\left(y=c_{k}\right) \prod_{j=1}^{n} p\left(x_{j} \mid y=c_{k}\right)
y ^ = arg c k max p ( y = c k ) j = 1 ∏ n p ( x j ∣ y = c k )
讲真的,就是一坨屎,我也不想看
举个栗子(99%
问题背景
某个医院早上来了六个门诊的病人,他们的情况如下表所示:
症状
职业
病情
打喷嚏
护士
感冒
打喷嚏
农夫
过敏
头痛
建筑工人
脑震荡
头痛
建筑工人
感冒
打喷嚏
教师
感冒
头痛
教师
脑震荡
现在又来了第七个病人,是一个 打喷嚏的建筑工人 。请问他患上 感冒 的概率有多大?
ans
根据贝叶斯定理:
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) \mathrm{P}(\mathrm{A} \mid \mathrm{B})=\frac{\mathrm{P}(\mathrm{B} \mid \mathrm{A}) \mathrm{P}(\mathrm{A})}{\mathrm{P}(\mathrm{B})}
P ( A ∣ B ) = P ( B ) P ( B ∣ A ) P ( A )
可得:
P (感冒|打喷嚏 x 建筑工人 ) = P ( 打喷嚏 x 建筑工人|感冒 ) × P ( 感冒 ) P ( 打喷嚏 x 建筑工人 ) \begin{array}{l}
\mathrm{P} \text { (感冒|打喷嚏 } \mathrm{x} \text { 建筑工人 }) \\
=\frac{P(\text { 打喷嚏 } \mathrm{x} \text { 建筑工人|感冒 }) \times \mathrm{P}(\text { 感冒 })}{\mathrm{P}(\text { 打喷嚏 } \mathrm{x} \text { 建筑工人 })} \\
\end{array}
P ( 感冒 | 打喷嚏 x 建筑工人 ) = P ( 打喷嚏 x 建筑工人 ) P ( 打喷嚏 x 建筑工人 | 感冒 ) × P ( 感冒 )
根据朴素贝叶斯条件独立性的假设可知,"打喷嚏"和"建筑工人"这两个特征是独立的 ,因此,上面的等式就变成了
P ( 感冒|打喷喷 x 建筑工人 ) = P ( 打喷嗦|感冒 ) × P ( 建筑工人|感冒 ) × P ( 感冒 ) P ( 打喷喗 ) × P ( 建筑工人 ) \begin{array}{l}
P(\text { 感冒|打喷喷 } x \text { 建筑工人 }) \\
=\frac{P(\text { 打喷嗦|感冒 }) \times P(\text { 建筑工人|感冒 }) \times P(\text { 感冒 })}{P(\text { 打喷喗 }) \times P(\text { 建筑工人 })}
\end{array}
P ( 感冒 | 打喷喷 x 建筑工人 ) = P ( 打喷喗 ) × P ( 建筑工人 ) P ( 打喷嗦 | 感冒 ) × P ( 建筑工人 | 感冒 ) × P ( 感冒 )
所以:
P ( 感冒 ∣ 打喷軲 x 建筑工人 ) = 0.66 × 0.33 × 0.5 0.5 × 0.33 = 0.66 \mathrm{P}(\text { 感冒 } \mid \text { 打喷軲 } \mathrm{x} \text { 建筑工人 })=\frac{0.66 \times 0.33 \times 0.5}{0.5 \times 0.33}=0.66
P ( 感冒 ∣ 打喷軲 x 建筑工人 ) = 0.5 × 0.33 0.66 × 0.33 × 0.5 = 0.66
因此,这个打喷嚏的建筑工人,有66%的概率是得了感冒。同理,可以计算这个病人患上过敏或脑震荡的概率。比较这几个概率,就可以知道他最可能得什么病。
有没有感觉其实没有那么难
碎碎念
计算过程中有没有发现,对于打喷嚏和建筑工人这一特征组合,要计算属于某类结果时,分母实际上始终是固定的,因此,在编程实现的过程中,如果只是判断每一类概率的大小,完全不用计算分母,只需要计算并比较分子大小即可。(偷懒技能get
高斯朴素贝叶斯(99%
除了上述模型外,常见的朴素贝叶斯还有:高斯朴素贝叶斯 ,伯努利朴素贝叶斯 ,多项式朴素贝叶斯 。
之前分析的都是基于离散型变量,但实际应用过程中,连续型变量往往占据绝大部分。
适用于连续变量,其假定各个特征 𝑥 𝑖 𝑥_𝑖 x i 𝑦 𝑦 y 正态分布 的概率密度函数来计算概率。
G a u s s i a n N B i m p l e m e n t s t h e G a u s s i a n N a i v e B a y e s a l g o r i t h m f o r c l a s s i f i c a t i o n . T h e l i k e l i h o o d o f t h e f e a t u r e s i s a s s u m e d t o b e G a u s s i a n : P ( x i ∣ y ) = 1 2 π σ y 2 exp ( − ( x i − μ y ) 2 2 σ y 2 ) T h e p a r a m e t e r s σ y a n d μ y a r e e s t i m a t e d u s i n g m a x i m u m l i k e l i h o o d . GaussianNB\ implements\ the\ Gaussian\ Naive\ Bayes\ algorithm\ for\ classification.\\ The\ likelihood\ of\ the\ features\ is\ assumed\ to\ be\ Gaussian:\\
P\left(x_{i} \mid y\right)=\frac{1}{\sqrt{2 \pi \sigma_{y}^{2}}} \exp \left(-\frac{\left(x_{i}-\mu_{y}\right)^{2}}{2 \sigma_{y}^{2}}\right)\\
The\ parameters\ \sigma_{y}\ and\ \mu_{y}\ are\ estimated\ using\ maximum\ likelihood.
G a u ss ian NB im pl e m e n t s t h e G a u ss ian N ai v e B a yes a l g or i t hm f or c l a ss i f i c a t i o n . T h e l ik e l ih oo d o f t h e f e a t u res i s a ss u m e d t o b e G a u ss ian : P ( x i ∣ y ) = 2 π σ y 2 1 exp ( − 2 σ y 2 ( x i − μ y ) 2 ) T h e p a r am e t ers σ y an d μ y a re es t ima t e d u s in g ma x im u m l ik e l ih oo d .
(为什么有英文解释啊喂:为平庸的复习材料加一点逼格,嘘
其中:
μ y \mu_y μ y y y y x − i i x_{-} i_{i} x − i i σ y \sigma_y σ y y y y x − i x_{-} i x − i
其实就是多背一个公式啦。
python实现(50%
虽然他说可能会考,但我觉得考的可能性不大,可以跳过其实
注释我也懒得写了(英文注释是 copilot 补全的
接下来就使用 numpy 和 pandas 实现一下朴素贝叶斯。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 def nb_fit (X, y ): """ X: pandas.DataFrame, the training data y: pandas.DataFrame, the target """ classes = y[y.columns[0 ]].unique() class_count = y[y.columns[0 ]].value_counts() class_prior = class_count/len (y) prior = dict () for col in X.columns: for j in classes: p_x_y = X[(y==j).values][col].value_counts() for i in p_x_y.index: prior[(col, i, j)] = p_x_y[i]/class_count[j] return classes, class_prior, prior def predict (X_test ): """ X_test: pandas.DataFrame, the test data """ res = [] for c in classes: p_y = class_prior[c] p_x_y = 1 for i in X_test.items(): p_x_y *= prior[tuple (list (i)+[c])] res.append(p_y*p_x_y) return classes[np.argmax(res)]
总结
N a v i e B a y e s Navie\ Bayes N a v i e B a yes
优点
生成式模型,通过计算概率来进行分类,可以用来处理多分类问题。
对小规模的数据表现很好,适合多分类任务,适合增量式训练,算法也比较简单。
缺点
对输入数据的表达形式很敏感。(离散型或连续型
由于朴素贝叶斯的“朴素”特点,所以会带来一些准确率上的损失。
需要计算先验概率,分类决策存在错误率。
朴素贝叶斯为什么 “朴素 ”
当我们假设特征相互独立时,我们只能把总的条件概率写成特征的个别条件概率的乘积。这是我们在这里做的“天真”假设,是为了让贝叶斯定理对我们有用。
但是,在现实生活中,当特性彼此独立时,几乎从来没有这种情况。功能中总是有某种依赖关系。例如,如果一个特征是一个人的年龄,而另一个特征是年薪,那么在大多数情况下都有明显的依赖关系。
然而,我们仍然继续把这个定理应用于分类问题,例如文本分类、垃圾邮件过滤等,它的效果出奇的好!