支持向量机–SVM与核学习–kernel

原话说的是，主要考察思想…\ …你搁这搁这呢

讨论最基本的二分类的支持向量机（support vector machines,SVMsupport\ vector\ machines, SVM），考虑训练样本集 D=(x1→,y1),…,(xm→,ym),yi∈−1,+1D=\left(\overrightarrow{x_{1}}, y_{1}\right), \ldots,\left(\overrightarrow{x_{m}}, y_{m}\right), y_{i} \in-1,+1 。从最基本的超平面划分训练样本开始，导出 SVMSVM 的基本问题，再利用对偶问题求解，最后讨论 SVMSVM 的核技巧。

SVM

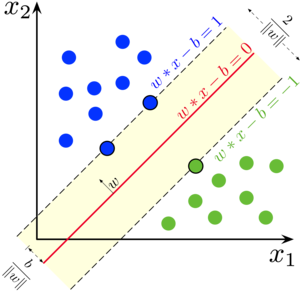
超平面

超平面（Hyper Plane） 是在样本空间中的一个平面。在我们熟悉的二维平面上, 一条直线的方程可以表示为 ax+by+c=0a x+b y+c=0, 推广到多维的情况之后，超平面 可以用向量的形式表示为 w⃗⋅x⃗+b=0\vec{w} \cdot \vec{x}+b=0 , 记为 (w⃗,b\vec{w}, b) 的形式，其中 w⃗\vec{w} 是法向 量，而 bb 为位移项。
考虑任意一点 x⃗\vec{x} 到超平面之间的距离，可以表示为:

γ=∣w⃗⋅x⃗+b∣∥w⃗∥\gamma=\frac{|\vec{w} \cdot \vec{x}+b|}{\|\vec{w}\|}

超平面能将样本空间划分成两部分。假设超平面 (w⃗,b\vec{w}, b) 将所有样本正确分类, 即对于任意的 (xi→,yi)∈D\left(\overrightarrow{x_{i}}, y_{i}\right) \in D, 若 yi=+1y_{i}=+1 , 那么 w⃗⋅x⃗+b>0\vec{w} \cdot \vec{x}+b>0 , 若 yi=−1y_{i}=-1, 那 么 w⃗⋅x⃗+b<0\vec{w} \cdot \vec{x}+b<0。像这样的决策函数可以表示为:

yi=sign⁡(w⃗⋅xi→+b)y_{i}=\operatorname{sign}\left(\vec{w} \cdot \overrightarrow{x_{i}}+b\right)

那么，在一个空间中，会存在多个超平面能够将训练样本分开，那么究竟该努力去 找哪一个超平面呢?

最大间隔

对于 (x⃗i,yi)\left(\vec{x}_{i}, y_{i}\right), 可以将上面的距离公式的分子部分代入 yiy_{i} 改写成:

γi=yi(w⃗⋅x⃗+b)∥w⃗∥\gamma_{i}=\frac{y_{i}(\vec{w} \cdot \vec{x}+b)}{\|\vec{w}\|}

定义间隔（marginmargin）γ\gamma 为所有样本中离超平面最近的那个, 即 γ=min⁡γi\gamma=\min \gamma_{i}, 那 么 γi≥γ\gamma_{i} \geq \gamma 总是成立的，代入上式可得:

yi(w⃗⋅x⃗+b)∥w⃗∥≥γ\frac{y_{i}(\vec{w} \cdot \vec{x}+b)}{\|\vec{w}\|} \geq \gamma

因此，SVMSVM 的问题就变成了找到 “最大间隔”（maximum marginmaximum\ margin）的超平 面，使得 γ\gamma 最大，即:

max⁡(w⃗,b)min⁡i1∥w⃗∥∣w⃗⋅x⃗i+b∣ s.t. yi(w⃗⋅x⃗i+b)>0,i=1,2,…,m\begin{array}{l} \max _{(\vec{w}, b)} \min _{i} \frac{1}{\|\vec{w}\|}\left|\vec{w} \cdot \vec{x}_{i}+b\right| \\ \text { s.t. } \quad y_{i}\left(\vec{w} \cdot \vec{x}_{i}+b\right)>0, \quad i=1,2, \ldots, m \end{array}

因为间隔始终大于 0 , 即 ∣w⃗⋅x⃗i+b∣>0\left|\vec{w} \cdot \vec{x}_{i}+b\right|>0, 则可以通过缩放 (w⃗,b\vec{w}, b) 使得 min⁡i∣w⃗⋅x⃗i+b∣=1\min _{i}\left|\vec{w} \cdot \vec{x}_{i}+b\right|=1, 那么上面的问题就变成 max⁡1∥w⃗∥\max \frac{1}{\|\vec{w}\|}, 即 min⁡∥w⃗∥\min \|\vec{w}\|, 在其它书里通常会被等价成 min⁡12∥w⃗∥2\min \frac{1}{2}\|\vec{w}\|^{2}, 于是上式可以重写成:

min⁡12∥w⃗∥2 s.t. yi(w⃗⋅x⃗i+b)≥1,i=1,2,…,m\begin{array}{ll} \min & \frac{1}{2}\|\vec{w}\|^{2} \\ \text { s.t. } & y_{i}\left(\vec{w} \cdot \vec{x}_{i}+b\right) \geq 1, \quad i=1,2, \ldots, m \end{array}

是一个凸二次规划（convex quadratic programmingconvex\ quadratic\ programming）问题，这样就能够利用 上现有的求解优化问题的方法。（没错，就是一个运筹学的线性规划问题）

对偶问题

浅浅回顾一下

首先考虑一个最优化问题:

min⁡f(z⃗) s.t. hi(z⃗)≤0\begin{array}{l} \min f(\vec{z}) \\ \text { s.t. } \quad h_{i}(\vec{z}) \leq 0 \end{array}

引入拉格朗日函数 L(z⃗,α⃗)\mathcal{L}(\vec{z}, \vec{\alpha}), 其中 α⃗=(α1,…,αm),αi≥0\vec{\alpha}=\left(\alpha_{1}, \ldots, \alpha_{m}\right), \alpha_{i} \geq 0 为拉格朗日乘 子，则有：

L(z⃗,α⃗)=f(z⃗)+∑αihi(z⃗)\mathcal{L}(\vec{z}, \vec{\alpha})=f(\vec{z})+\sum \alpha_{i} h_{i}(\vec{z})

那么上面的最优化问题等价于：

min⁡z⃗max⁡α⃗≥0L(z⃗,α⃗)\min _{\vec{z}} \max _{\vec{\alpha} \geq 0} \mathcal{L}(\vec{z}, \vec{\alpha})

称为 原始问题（primal problemprimal\ problem。下面来证明其等价于一开始的优化问题，主要思路是将拉格朗日函数展开代入，再利用 α⃗≥0\vec{\alpha} \geq 0 的条件消去第二项：

min⁡z⃗max⁡α⃗≥0L(z⃗,α⃗)=min⁡z⃗(f(z⃗)+max⁡α⃗≥0∑αihi(z⃗))=min⁡z⃗(f(z⃗)+{0, if hi(z⃗)≤0∞, if hi(z⃗)>0)=min⁡z⃗f(z⃗)\begin{aligned} & \min _{\vec{z}} \max _{\vec{\alpha} \geq 0} \mathcal{L}(\vec{z}, \vec{\alpha}) \\ = & \min _{\vec{z}}\left(f(\vec{z})+\max _{\vec{\alpha} \geq 0} \sum \alpha_{i} h_{i}(\vec{z})\right) \\ = & \min _{\vec{z}}\left(f(\vec{z})+\left\{\begin{array}{ll} 0, & \text { if } h_{i}(\vec{z}) \leq 0 \\ \infty, & \text { if } h_{i}(\vec{z})>0 \end{array}\right)\right. \\ = & \min _{\vec{z}} f(\vec{z}) \end{aligned}

将该问题的中的 min⁡\min 和 max⁡\max 交换位置，即可得到其对偶问题（dual problemdual\ problem）:

max⁡α⃗≥0min⁡z⃗L(z⃗,α⃗)\max _{\vec{\alpha} \geq 0} \min _{\vec{z}} \mathcal{L}(\vec{z}, \vec{\alpha})

原始问题与对偶问题的关系:

max⁡α⃗≥0min⁡z⃗L(z⃗,α⃗)≤min⁡z⃗max⁡α⃗≥0L(z⃗,α⃗)\max _{\vec{\alpha} \geq 0} \min _{\vec{z}} \mathcal{L}(\vec{z}, \vec{\alpha}) \leq \min _{\vec{z}} \max _{\vec{\alpha} \geq 0} \mathcal{L}(\vec{z}, \vec{\alpha})

在某些条件下，原始问题与对偶问题的最优值相等，这时候可以用解对偶问题代替 解原始问题。该条件称为 KKT（Karush-Kunh-Tucker）条件，具体证明超出了本文的涉及范围，我自己也不会，就先略过。在这个条件下，可以从 SVMSVM 问题的 对偶问题 求解，进而得到 SVMSVM 的解。

SVM 求解（99%

将 SVMSVM 的问题用拉格朗日函数的形式重写为:

L(w⃗,b,α⃗)=12∥w⃗∥2⏟f(w⃗,b)+∑αi(1−yi(w⃗⋅x⃗i−b))⏟hi(w⃗,b)≤0\mathcal{L}(\vec{w}, b, \vec{\alpha})=\underbrace{\frac{1}{2}\|\vec{w}\|^{2}}_{f(\vec{w}, b)}+\sum \alpha_{i} \underbrace{\left(1-y_{i}\left(\vec{w} \cdot \vec{x}_{i}-b\right)\right)}_{h_{i}(\vec{w}, b) \leq 0}

令 L(w⃗,b,α⃗)\mathcal{L}(\vec{w}, b, \vec{\alpha}) 对于 w⃗\vec{w} 和 bb 的偏导数等于零:

{∂L∂w⃗=w⃗−∑αiyix⃗i=0∂L∂b=∑αiyi=0\left\{\begin{array}{l} \frac{\partial \mathcal{L}}{\partial \vec{w}}=\vec{w}-\sum \alpha_{i} y_{i} \vec{x}_{i}=0 \\ \frac{\partial \mathcal{L}}{\partial b}=\sum \alpha_{i} y_{i}=0 \end{array}\right.

可得：

w⃗=∑αiyix⃗i0=∑αiyi\begin{aligned} \vec{w} & =\sum \alpha_{i} y_{i} \vec{x}_{i} \\ 0 & =\sum \alpha_{i} y_{i} \end{aligned}

将上式代入 L(w⃗,b,α⃗)\mathcal{L}(\vec{w}, b, \vec{\alpha}) 可得:

L(w⃗,b,α⃗)=12(∑αiyix⃗i)⋅(∑αiyix⃗i)+∑αi(1−yi((∑αiyix⃗i)⋅x⃗i−b)))=∑i=1mαi−12∑i=1m∑j=1mαiαjyiyj(x⃗i⋅x⃗j)\begin{aligned} \mathcal{L}(\vec{w}, b, \vec{\alpha})= & \frac{1}{2}\left(\sum \alpha_{i} y_{i} \vec{x}_{i}\right) \cdot\left(\sum \alpha_{i} y_{i} \vec{x}_{i}\right) \\ & \left.+\sum \alpha_{i}\left(1-y_{i}\left(\left(\sum \alpha_{i} y_{i} \vec{x}_{i}\right) \cdot \vec{x}_{i}-b\right)\right)\right) \\ = & \sum_{i=1}^{m} \alpha_{i}-\frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(\vec{x}_{i} \cdot \vec{x}_{j}\right) \end{aligned}

这样，对偶问题就变成:

max⁡α⃗≥0min⁡z⃗L(z⃗,α⃗)⟹max⁡α⃗≥0∑i=1mαi−12∑i=1m∑j=1mαiαjyiyj(x⃗i⋅x⃗j) s.t. ∑αiyi=0,αi≥0\begin{aligned} & \max _{\vec{\alpha} \geq 0} \min _{\vec{z}} \mathcal{L}(\vec{z}, \vec{\alpha}) \\ \Longrightarrow & \max _{\vec{\alpha} \geq 0} \sum_{i=1}^{m} \alpha_{i}-\frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(\vec{x}_{i} \cdot \vec{x}_{j}\right) \\ & \text { s.t. } \quad \sum \alpha_{i} y_{i}=0, \alpha_{i} \geq 0 \end{aligned}

解出 α⃗\vec{\alpha} 后，求出 w⃗\vec{w} 与 bb 即可得到模型:

f(x⃗)=w⃗⋅x⃗+b=∑i=1mαiyi(x⃗i⋅x⃗)+b\begin{aligned} f(\vec{x}) & =\vec{w} \cdot \vec{x}+b \\ & =\sum_{i=1}^{m} \alpha_{i} y_{i}\left(\vec{x}_{i} \cdot \vec{x}\right)+b \end{aligned}

具体求解过程需要满足上面提到的 KTTKTT 条件:

{αi≥0yif(x⃗i)−1≥0αi(yif(x⃗i)−1)=0\left\{\begin{array}{l} \alpha_{i} \geq 0 \\ y_{i} f\left(\vec{x}_{i}\right)-1 \geq 0 \\ \alpha_{i}\left(y_{i} f\left(\vec{x}_{i}\right)-1\right)=0 \end{array}\right.

求解上面的对偶问题 的一个著名算法是 SMO (Sequential Minimal Optimization), 这里不展开叙述。

软间隔

啥是软间隔，就是近似线性可分问题

上面我们考虑的都是数据可以分隔的情况，那么当数据集并不是完全能被超平面分 隔，即有些点不满足约束 yi(w⃗⋅x⃗i+b)≥1y_{i}\left(\vec{w} \cdot \vec{x}_{i}+b\right) \geq 1, 那可以设定一个惩罚项：

ξi=max⁡{1−yi(w⃗⋅x⃗i+b),0}\xi_{i}=\max \left\{1-y_{i}\left(\vec{w} \cdot \vec{x}_{i}+b\right), 0\right\}

那么原来的 SVMSVM 的优化问题就会变成：

min⁡w⃗,b12∥w⃗∥2+C∑i=1mmax⁡{1−yi(w⃗⋅x⃗i+b),0} s.t. 1−yi(w⃗⋅x⃗i+b)≤0,i=1,2,…,m\begin{array}{ll} \min _{\vec{w}, b} & \frac{1}{2}\|\vec{w}\|^{2}+C \sum_{i=1}^{m} \max \left\{1-y_{i}\left(\vec{w} \cdot \vec{x}_{i}+b\right), 0\right\} \\ \text { s.t. } & 1-y_{i}\left(\vec{w} \cdot \vec{x}_{i}+b\right) \leq 0, \quad i=1,2, \ldots, m \end{array}

其中的 max⁡(1−z,0)\max (1-z, 0) 称为 “折页损失” （hinge losshinge\ loss）。接着引入 “松他变量” (slackvariable)ξi≥0(slack variable) \xi_{i} \geq 0, 将上式重写为:

min⁡w⃗,b12∥w⃗∥2+C∑i=1mξi s.t. yi(w⃗⋅x⃗i+b)≥1−ξiξi≥0,i=1,2,…,m\begin{array}{ll} & \min _{\vec{w}, b} \frac{1}{2}\|\vec{w}\|^{2}+C \sum_{i=1}^{m} \xi_{i} \\ \text { s.t. } & y_{i}\left(\vec{w} \cdot \vec{x}_{i}+b\right) \geq 1-\xi_{i} \\ & \xi_{i} \geq 0, i=1,2, \ldots, m \end{array}

即可得到 “软间隔支持向量机” (soft margin SVMsoft\ margin\ SVM)。求解方法与前面是一样的。

核方法（99%

ppt 看的头大

当遇到样本是 非线性可分 时，一般的线性 SVMSVM 就无法很好的分类，这时候可以采用核技巧（kerneltrickkernel trick）。

基本思想是 将样本映射至高维空间，变成高维空间中线性可分的即可。

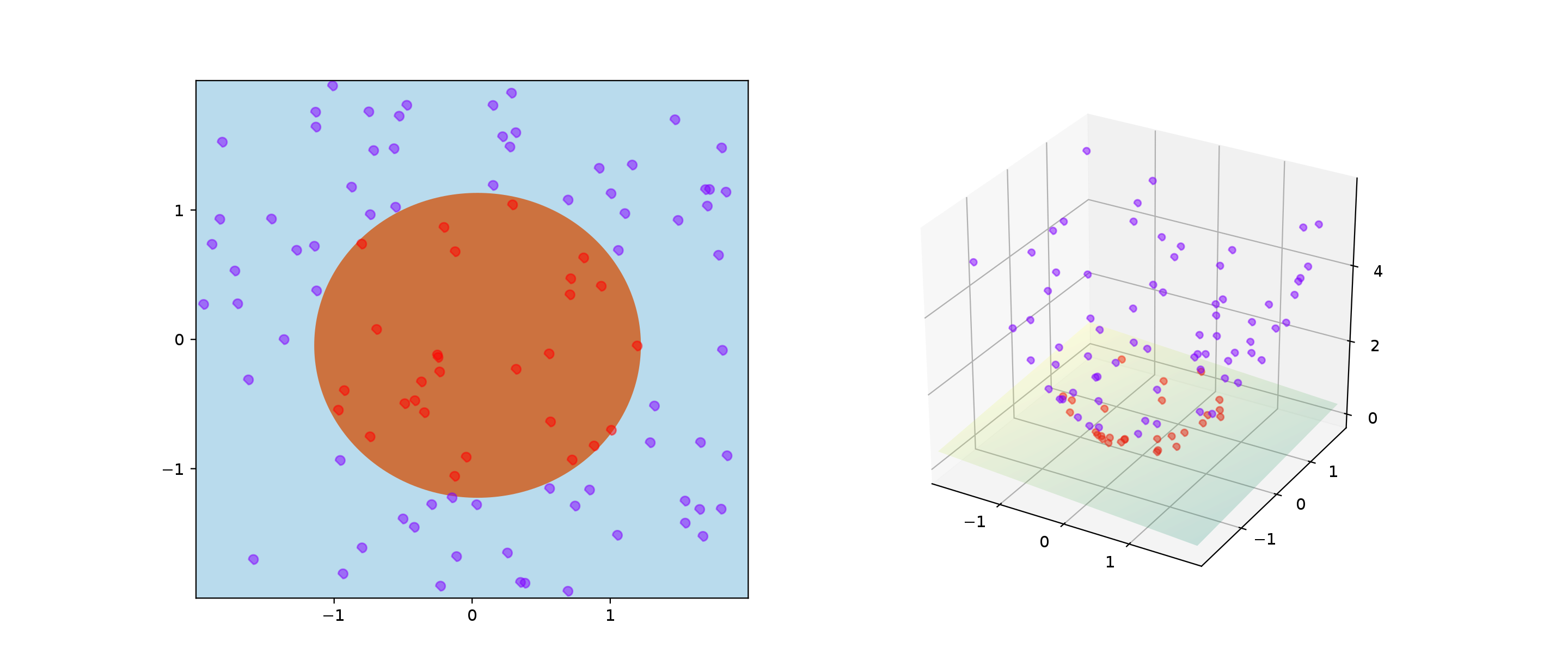
kernel

考虑一个映射函数 ϕ(x⃗)\phi(\vec{x}), 将 dd 维特征映射至 mm 维:

ϕ(x⃗):Rd→Rm\phi(\vec{x}): \mathbb{R}^{d} \rightarrow \mathbb{R}^{m}

定义 核函数（kernel functionkernel\ function）:

K(x⃗i,x⃗j)=ϕ(x⃗i)⋅ϕ(x⃗j)K\left(\vec{x}_{i}, \vec{x}_{j}\right)=\phi\left(\vec{x}_{i}\right) \cdot \phi\left(\vec{x}_{j}\right)

核技巧的思想是用核函数 KK 避免在高维 mm 空间中计算映射函数的内积，这样能 够极大简化运算。
根据 Mercer′s theoremMercer's\ theorem, 函数 KK 能够满足成为核函数的充分必要条件是 KK 是 半正定（positive semidefinitepositive\ semidefinite），即

∑i,j=1mcicjK(x⃗i,x⃗j)≥0\sum_{i, j=1}^{m} c_{i} c_{j} K\left(\vec{x}_{i}, \vec{x}_{j}\right) \geq 0

常用的核函数有 多项式核函数（Polynomial functionPolynomial\ function）:

K(x⃗i,x⃗j)=(x⃗i⋅x⃗j+1)dK\left(\vec{x}_{i}, \vec{x}_{j}\right)=\left(\vec{x}_{i} \cdot \vec{x}_{j}+1\right)^{d}

以及 高斯核函数（Guassian radial basis functionGuassian\ radial\ basis\ function），通常称为 RBF KernelRBF\ Kernel:

K(x⃗i,x⃗j)=exp⁡(−∥x⃗i−x⃗j∥22σ2)K\left(\vec{x}_{i}, \vec{x}_{j}\right)=\exp \left(-\frac{\left\|\vec{x}_{i}-\vec{x}_{j}\right\|^{2}}{2 \sigma^{2}}\right)