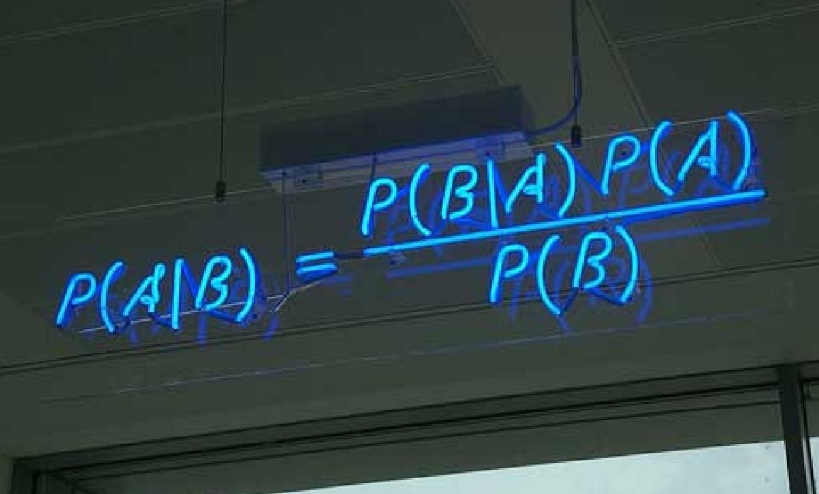ML

~~声明：该系列完全为了应付期末考准备的，大部分都是按照自己方便理解和复习来写的，专业性不足，但应付 FZU 还是绰绰有余。~~

对于一些非人化的、wsp所谓美的公式，我尽量用人话表达出来

标题后面的百分号为会考的概率。（基于贝叶斯估计的概率 ~~吹牛谁不会啊~~

导论

机器学习定义（80%

对于某类任务T 和性能度量 P，如果一个计算机程序在 T 上以 p 衡量的性能随着经验 E 而自我完善，那么称这个计算机程序在从经验 E 中学习。
$<P, T, E>$

分类

监督学习
- 分类、回归、降维
无监督学习
- 密度估计、聚类、降维、图像分割
弱监督学习
- 半监督学习、偏监督学习
增强学习
- $Q-learnign$

监督学习和无监督学习概念（80%

监督学习（ $supervised learning$ ）
- 监督学习 是对具有概念标记（分类）的训练样本进行学习，以尽可能对训练样本集外的数据进行标记（分类）预测。
- 监督学习的任务是学习一个模型，使模型能够对任意给定的输入，对其相应的输出做出一个好的预测。即 利用训练数据集学习一个模型，再用模型对测试样本集进行预测。
无监督学习（ $unsupervised learning$ ）
- 无监督学习 是对没有概念标记（分类）的训练样本进行学习，以发现训练样本集中的结构性知识。
- 非监督学习为直接对数据进行建模。没有给定事先标记过的训练范
两者区别

监督学习	无监督学习
目的明确的训练方式，知道得到的是什么	没有明确的目标，训练前不知道结果是什么
需要提前给训练集打标签	无需提前打标签
由于目标明确，可以衡量效果	几乎无法量化预测效果如何

KNN

$KNN$ 是一个 监督学习 的分类算法。

基本思想

如果一个样本在特征空间中的 $k$ 个最邻近的样本中的大多数属于某一个类别，则该样本也划分为这个类别。

$KNN$ 算法中，所选择的邻居都是 已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

$e.g.$

knn

样本点间距离的选取（99%

常用距离度量方法：

欧几里得距离、曼哈顿距离、余弦值、相关度 … …

欧几里得距离（99%

$Euclidean Distance$ 定义

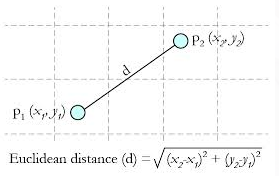
两个点或元组 $P_1 =(x_1，y_1)$ 和 $P_2 = (x_2，y_2)$ 的欧几里得距离定义为：

对于样本空间中的两个点 $X = (x_1, x_2, \dots , x_n)$ 和 $Y = (y_1, y_2, \dots, y_n)$ ，其欧几里得距离为：

$E(X, Y) = \sqrt{\sum^n_{i=1}(x_i - y_i)^2}$

曼哈顿距离（50%

$dist(X, Y) = \sum_{i=1}^n |x_i - y_i|$

算法步骤

计算测试数据与各个训练数据之间的距离
按照距离的递增关系进行排序
选取距离最小的 $k$ 个点
确定前 $k$ 个点所在类别的出现频率
返回前 $k$ 个点中出现频率最高的类别作为测试数据的预测分类

代码实现、手搭（99%

~~考的只会是算法中的和核心部分~~

计算多维度的两个点之间的欧氏距离

def euclideanDistance(instance1, instance2, length):
    """计算样本空间中两个点的欧氏距离

    Args:
        instance1 (array): 样本点1
        instance2 (array): 样本点2
        length (int): 样本点维度

    Returns:
        double: 两样本点的欧氏距离
    """    
    distance = 0
    for x in range(length):
        distance += pow((instance1[x]-instance2[x]), 2)
    return math.sqrt(distance)

获取与待测样本点距离最近的 $k$ 个点

def getNeighbors(trainingSet, testInstance, k):
    """获取待测样本点最近的k个邻居

    Args:
        trainingSet (set): 训练样本点集
        testInstance (array): 待测样本点
        k (int): KNN的k值

    Returns:
        array: 距离待测样本点最近的k个邻居
    """    
    distances = []
    length = len(testInstance)-1
    for x in range(len(trainingSet)):
        dist = euclideanDistance(testInstance, trainingSet[x], length)
        distances.append((trainingSet[x], dist))   #获取到测试点到其他点的距离
    distances.sort(key=operator.itemgetter(1))    #对所有的距离进行排序
    neighbors = []
    for x in range(k):   #获取到距离最近的k个点
        neighbors.append(distances[x][0])
        return neighbors

得到 $k$ 个邻居中占比最高的类别（本质就是选举过程）

def getResponse(neighbors):
    """得到k个邻居中占比最高的类别

    Args:
        neighbors (array): 距离最近的k个邻居

    Returns:
        string: 占比最高的类别
    """    
    classVotes = {}
    for x in range(len(neighbors)):
        response = neighbors[x][-1]  #获取第x个邻居的类别
        if response in classVotes:
            classVotes[response] += 1
        else:
            classVotes[response] = 1
    sortedVotes = sorted(classVotes.items(), key=operator.itemgetter(1), reverse=True)
    return sortedVotes[0][0]   #获取到票数最多的类别

关于 k 的取值

$k$ ：临近数，即在预测目标点时取几个临近的点来预测。

$k$ 取值的影响

若 $k$ 过小，一旦有噪声得成分存在们将会对预测产生比较大影响，例如取 $k$ 值为1时，一旦最近的一个点是噪声，那么就会出现偏差， $k$ 值的减小就意味着整体模型变得复杂，容易发生过拟合
如果 $k$ 的值取的过大时，就相当于用较大邻域中的训练实例进行预测，学习的近似误差会增大。这时与输入目标点较远实例也会对预测起作用，使预测发生错误。 $k$ 值的增大就意味着整体的模型变得简单

$k$ 的取值尽量要取奇数，以保证在计算结果最后会产生一个较多的类别，如果取偶数可能会产生相等的情况，不利于预测

$k$ 的取法

常用的方法是从 $k=1$ 开始，使用检验集估计分类器的误差率。重复该过程，每次 $k$ 增值1，允许增加一个近邻。选取产生最小误差率的 $k$ 。

一般 $k$ 的取值不超过20，上限是 $n$ （训练集样本点个数）的开方，随着数据集的增大， $k$ 的值也要增大。

总结

$KNN$ 算法是最简单有效的分类算法，简单且容易实现。当训练数据集很大时，需要大量的存储空间，而且需要计算待测样本和训练数据集中所有样本的距离，所以非常耗时
$KNN$ 对于随机分布的数据集分类效果较差，对于类内间距小，类间间距大的数据集分类效果好，而且对于边界不规则的数据效果好于线性分类器。
$KNN$ 对于样本不均衡的数据效果不好，需要进行改进。改进的方法时对 $k$ 个近邻数据赋予权重，比如距离测试样本越近，权重越大。
$KNN$ 很耗时，时间复杂度为 $O(n)$ ，一般适用于样本数较少的数据集，当数据量大时，可以将数据以树的形式呈现，能提高速度，常用的有 $kd-tree$ 和 $ball-tree$ 。